Deepseek GRPO 中的 KL Divergence

起

在 Deepseek R1 发布之后，看到了论文中 RL 的算法用的是 GRPO，而 GRPO 是在之前 Deepseek Math 的论文中被提出来的。GRPO 的目标函数如下：

$$\begin{array}{rl}{\mathcal{J}}_{GRPO}(\theta )& ={\mathbb{E}}_{[q\sim P(Q),\{o_i{\}}_{i=1}^G\sim {\pi }_{{\theta }_{old}}(O\mid q)]}\frac{1}{G}\sum _{i=1}^G\frac{1}{|o_i|}\sum _{t=1}^{|o_i|}\{min[\frac{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{{\theta }_{old}}(o_{i,t}\mid q,o_{i,<t})}{\hat{A}}_{i,t},\text{clip}(\frac{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{{\theta }_{old}}(o_{i,t}\mid q,o_{i,<t})},1-ϵ,1+ϵ){\hat{A}}_{i,t}]\\ & -\beta {\mathbb{D}}_{KL}[{\pi }_{\theta }\parallel {\pi }_{ref}]\}\end{array}$$

这里我们只看最后的 KL Divergence(KL 散度) 部分。关于最后 KL 散度的实现，论文特别做了说明：

And different from the KL penalty term used in PPO, we estimate the KL divergence with the following unbiased estimator (Schulman, 2020), which is guaranteed to be positive.

$${\mathbb{D}}_{KL}\left[{\pi }_{\theta }||{\pi }_{ref}\right]=\frac{{\pi }_{ref}(o_{i,t}|q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}-\log \frac{{\pi }_{ref}(o_{i,t}|q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}-1,$$

也就是说其使用的 KL Divergence 与 PPO 不同，GRPO 中采用了 Schulman 在博客 中提到的一个无偏估计。论文中使用的是博客中提到的$k_3$近似形式。让我们稍微展开一下这里的$k_3$近似。

首先 KL 散度的公式如下

$KL[q,p]=\sum _{x}q(x)\log \frac{q(x)}{p(x)}=E_{x\sim q}[\log \frac{q(x)}{p(x)}]$

定义

$$r=\frac{p(x)}{q(x)}$$

那么有

$$KL[q,p]=k_3=r-log(r)-1$$

因此，论文中的 ${\mathbb{D}}_{KL}\left[{\pi }_{\theta }||{\pi }_{ref}\right]$ 也可以写成下面由 $r$ 近似的形式：

$$\begin{array}{rl}{\mathbb{D}}_{KL}\left[{\pi }_{\theta }||{\pi }_{ref}\right]& =\frac{{\pi }_{ref}(o_{i,t}|q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}-\log \frac{{\pi }_{ref}(o_{i,t}|q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}-1\\ & =r-log(r)-1\end{array}$$

此时，

$$r=\frac{p(x)}{q(x)}=\frac{{\pi }_{ref}(o_{i,t}|q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}$$

对应地，

$$q(x)={\pi }_{\theta }(o_{i,t}|q,o_{i,<t})$$

$$p(x)={\pi }_{ref}(o_{i,t}|q,o_{i,<t})$$

到这里为止，论文中 KL 散度的推导的就完成了，一切都很清晰。后来我又读了几篇关于 KL 散度不对称性的博客，比如这篇Reverse vs Forward KL, 里面提到 Reverse KL Divergence 是类似${\mathbb{D}}_{KL}\left[q_{\varphi }||p\right]$的形式 (这里的$\varphi$是参数)，所以很自然地我认为${\mathbb{D}}_{KL}\left[{\pi }_{\theta }||{\pi }_{ref}\right]$就是 Reverse KL Divergence 的形式...直到我在 Twitter/X 上刷到一个帖子说 GRPO 用的是 Forward KL：

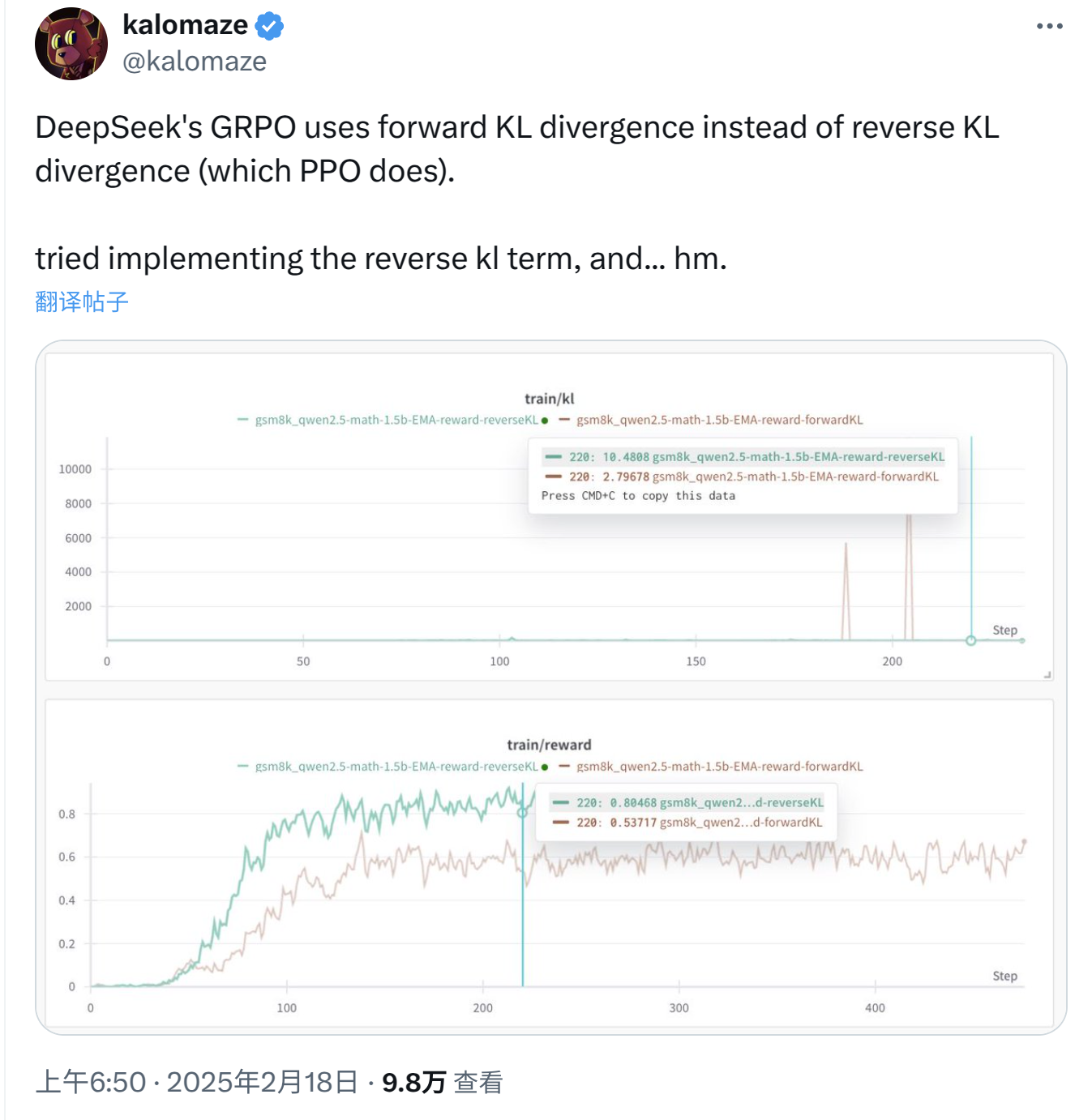
承

看到帖子的时候我就在想，这不可能啊，这么明显的错误评论区肯定有一堆人指正的。但事实是没有人反对，而且有两个哥们让人印象深刻：其中一个说，啊对对对，我们之前一篇论文也证明了 Forward 比 Reverse 更好；另外一个哥们是吟唱流，连发七八条帖子去分析。

到这里，我认识到可能是我错了，所以去请教 LLM 老师们，发现老师也都说 GRPO 就是用的 Forward KL。我郑重抗议说他们不对，应该是 Reverse KL，老师们并不接受...所以我开始反思我哪里想错了，并开始向认识的朋友们请教。（再次感谢各位！）不过辗转几次下来，好像也没什么定论。期间我又推导了几次，还是没找出哪里有问题。这个问题一直在我脑子里，就像一小朵乌云一样飘在那里，让我很是不好受......

转

紧接着 Grok3 发布了，我赶紧试了下这个问题。Grok3 告诉我说，GRPO 用的是 Reverse KL Divergence，分析的思路也都很正确。我开始意识到我可能并没错，错的是......

转折点是看到 Unsloth 发布的博客 Long-context GRPO，里面明确写道 GRPO 就是用的 Reverse KL Divergence：

The reference GRPO implementation uses the reverse KL divergence, not the forward KL divergence.

至此，我心中的那片乌云终于消失了...

既然谈到了 Reverse KL 和 Forward KL，不妨让我们更直观地理解一下两者的区别。下图来自博客Reverse vs Forward KL。

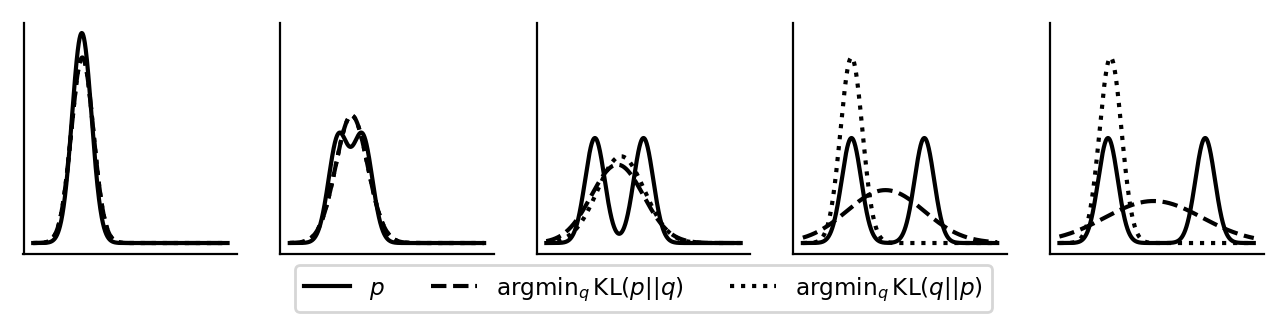
其中实线代表${\mathbb{D}}_{KL}\left[q_{\varphi }||p\right]$中$p$的分布，表示待逼近的分布。而$q_{\varphi }$则表示参数化的分布 (分布由$\varphi$决定)。最小化 DL 散度其实就是优化参数$\varphi$，使得最终的 KL 散度最小。下面长虚线是 Forward KL Divergence 为优化目标时的拟合结果；短虚线是 Reverse KL Divergence 为优化目标时的拟合结果。注意这里在模拟的时候，$p(x)$为混合高斯分布 (单峰或者双峰)，$q(x)$为普通的高斯分布 (单峰)，详见博客，此处不展开。

对于两者的区别，结论是：Reverse KL 的行为是 Zero-Forcing/Mode-Seeking；Forward KL 是 Mass-Covering/Mean-Seeking。

Reverse KL 的公式如下

$$\begin{array}{rl}KL[q,p]& =\sum _{x}q(x)\log \frac{q(x)}{p(x)}\\ & =\sum _{x}q(x)(\log q(x)-\log p(x))\end{array}$$

因为在$p(x)=0$的时候，$-\log p(x)$会趋近于无穷大，所以最小化 Reverse KL 的时候会强制将$q(x)$拉平到 0，这就是 Zero-Forcing。观察上图可以看到，实线为 0($p(x)=0$) 的时候，短虚线一定为 0.($q(x)=0$). 而为了让最终的 KL 散度尽可能地小，所以此时 Reverse KL 会尽可能找到一个峰去拟合，是为 Mode Seeking。

反观 Forward KL：

$$\begin{array}{rl}KL[p,q]& =\sum _{x}p(x)\log \frac{p(x)}{q(x)}\\ & =\sum _{x}p(x)(\log p(x)-\log q(x))\end{array}$$

因为是$p(x)$加权的，所以当$p(x)=0$的时候，随便$q(x)$呈现什么形态都不影响，因为对最终的 KL 散度贡献始终为 0，所以重点就就集中在$p(x)\ne 0$的部分。在$p(x)\ne 0$的部分尽可能地让两个分布的差距比较小，就诱导出了 Forward KL 的 Mass-Covering/Mean-Seeking 模式。

回到在 LLM 训练中，用 Reverse KL 和 Forward KL 有什么差别吗？Unsloth 其实给出了实验的分析，其实看结果似乎并没有太大的区别：

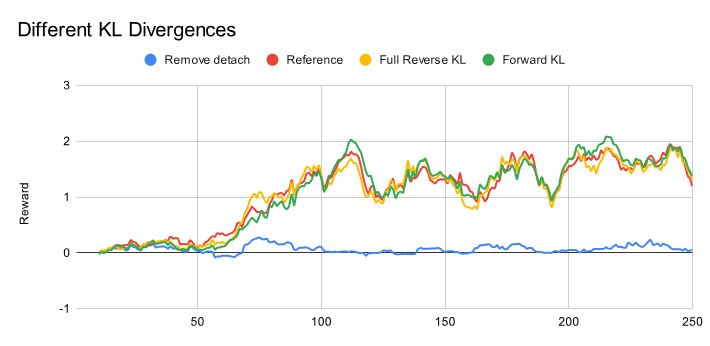
下面要说的是目前的一些猜想 (aka 暴论：)，笔者并没有去实际验证，仅作为拓展思考：这里 Reverse KL 和 Forward KL 没有差别的原因可能类似上面博客模拟实验中$p(x)$为单峰分布的情况，也就是说此时 LLM 输出 Token 的分布其实就是单峰的，这时候两个 KL 散度其实就是没有太多差别的。还是根据上面的模拟实验，在 LLM 的应用中，如果 Token 呈现多峰分布，此时两个 KL 的优化行为应该是不一样的：Reverse KL 的行为更加倾向于“锐化”原来的 Token 分布，也就是只保留那些概率很高的 Token，使得${\pi }_{\theta }$的行为和${\pi }_{ref}$尽可能一致；而 Forward KL 更倾向于探索一些中间地带的分布，进而使得${\pi }_{\theta }$会表现出${\pi }_{ref}$原本不会出现的模式。

合

回看这段颇有意思的经历，我逐渐明白社交网络的人多是为了自己，事实怎样对于他们来说是次要的。在 LLM 时代，受硬件的限制多少还有的，“Money is all your need”并非没有道理……很多想法没有显卡根本无从验证，在这个时候是选择相信自己的判断还是选择相信“主流的观点”是一个值得思考的问题。